TopOpt | 针对99行改进的88行拓扑优化程序完全注释
?博客搬家到自己搭建的 主页 啦q(≧▽≦q),大家快来逛逛鸭!
?
The Corresponding Files (Click to Save):
- Code? ? ? ? top88.m
- References? Efficient topology optimization in MATLAB using 88 lines of code
The Related Articals (Click in):
The program can be promoted by line:
88行程序为了提高效率,逻辑、流程没有99行程序那么清楚,建议初学先读99行。
?
| Modified SIMP方法中基于单元伪密度的杨氏弹性模量 | (1) | |
| 优化问题(柔度最小化)的数学表述 | (2) | |
| OC优化准则法更新设计变量 | (3) | |
| ? | (4) | |
| 目标函数关于设计变量的灵敏度信息 | (5) | |
| 体积约束关于设计变量的灵敏度信息 | (6) | |
| 对目标函数的灵敏度信息进行敏度滤波 | (7) | |
| 权重系数矩阵 | (8) | |
| 对设计变量进行密度滤波得到单元伪密度 | (9) | |
| 在密度滤波中,根据链式法则修正目标函数和体积约束关于设计变量的灵敏度信息 | (10) |
?

这里把有限元单元刚度矩阵的基础知识自己推导一遍就基本没问题了,网上很多资料,这里不多说了。这一段跟99行比大家都是构造矩阵,效率上没有什么太大的差距。
?
这里就拿4X3网格举例子了。程序注释上面有,很绕口,不如直观点来看看这三个矩阵到底在干嘛。注意nodenrs是节点编号,不是单元编号,nelx个单元一条边有(nelx+1)个节点这没什么好解释的。edofVec是所有单元第一个自由度,第一个自由度是啥,是左下角节点水平自由度。
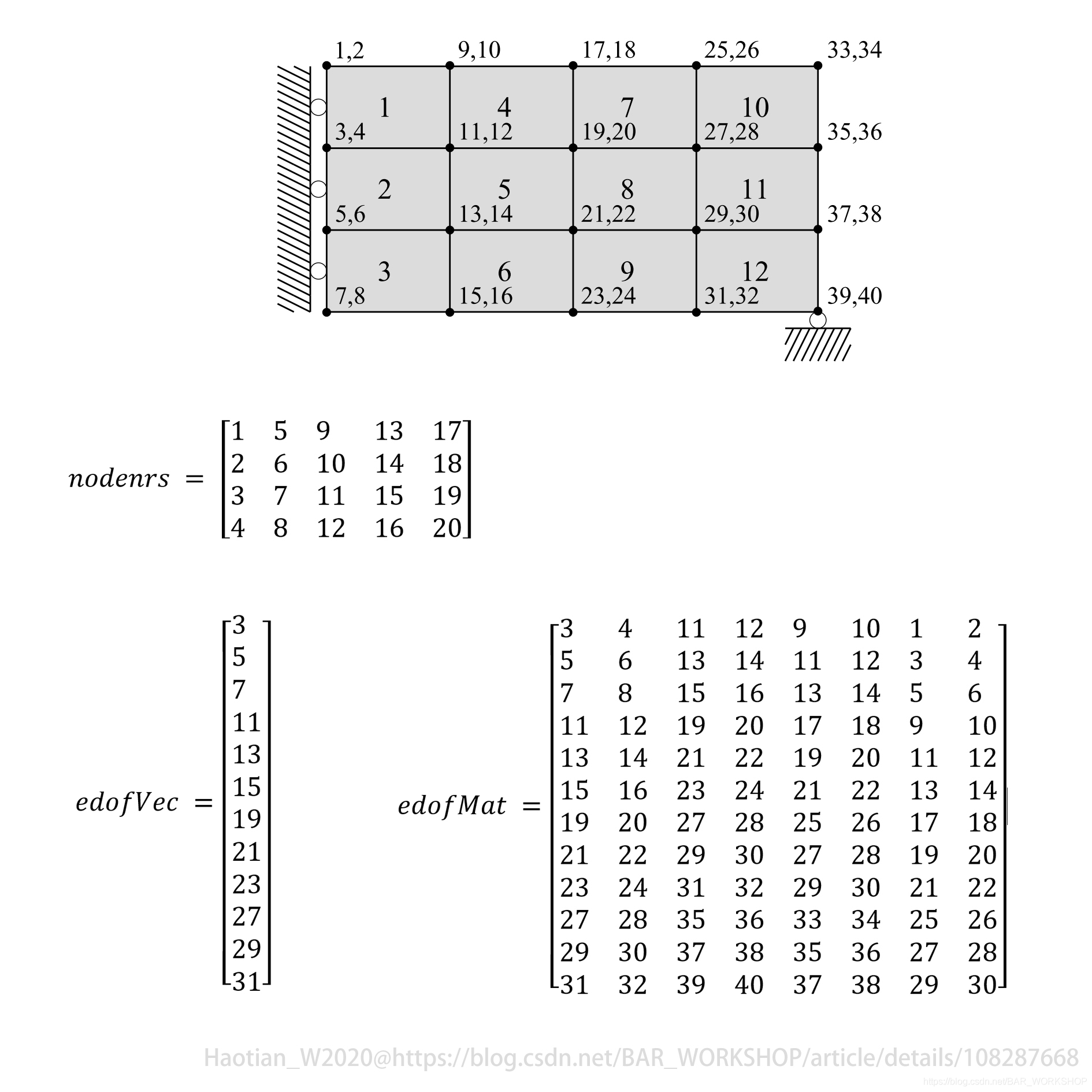
接下来细说从edofVec到edofMat怎么回事。 这里用到了repmat命令,具体去help,简单点理解成复制就好了。
这里只要理解透 “一个节点所有自由度 = 该节点第一个自由度 + 相对值” 就结束了。
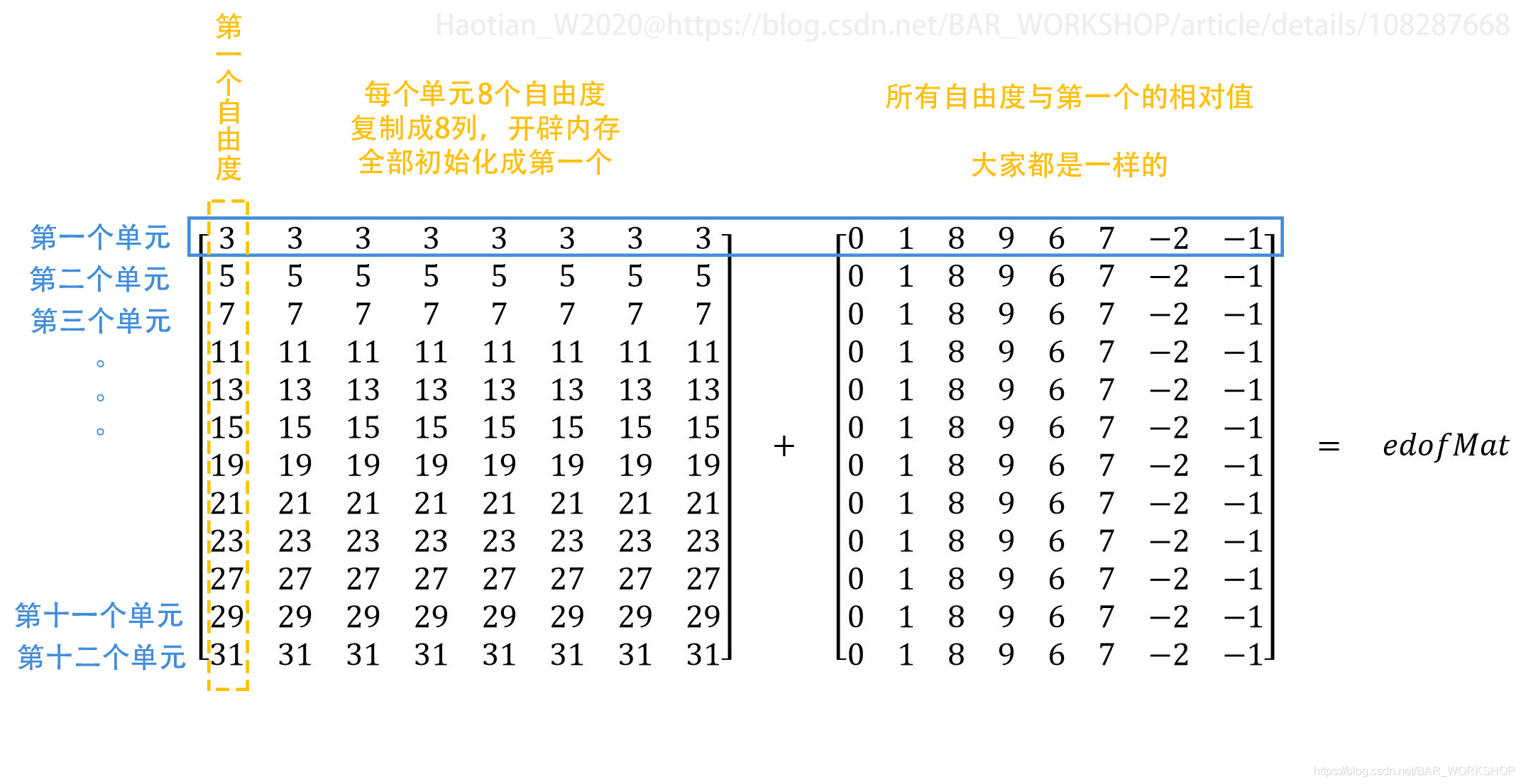
对应99行程序中 Line: 17-21遍历单元,当时的思路是遍历每个单元计算一下左上角、右上角节点编号,然后推算该单元所有自由度编号。
而在这里,88行程序中,作者使用矢量化思路,通过矩阵运算来提升程序运行效率。从上面我们也看到了,由于所有的单元大小形状都是一样的只有位置不一样,只要定了每个单元第一个自由度编号(图2 等号左边第一个矩阵),剩余的操作都是一样的(图2 等号左边第二个矩阵)。
下面是我写的一段测试代码,分别把99行和88行中相应片段粘贴过来,稍微修改使两段程序得到相同的结果。然后测试处理4万网格两者花费的时间。
从结果看,处理4万网格,矢量化程序运行时间不到遍历单元方法的万分之二,差异十分显著。况且,在99行程序中,每个迭代循环都要跑一次这个,如果有300次优化迭代那就要跑300次;而在88行程序中总共只需要在开头进行一次。这也就是为什么我用3700X处理器跑3万网格的99行程序要花掉我大半个下午,而同样3万网格的88行程序喝口水就能跑完。而且多次测试验证,网格越多,效率差距越大。
?
根据iK、jK和sK三元组生成总体刚度矩阵的稀疏矩阵K,索引向量iK和jK已经在循环体外面定义过了,sK需要在循环内确定。sK根据单元刚度矩阵KE和单元杨氏弹性模量求得,单元杨氏弹性模量参见论文公式(1)。
组装总体刚度矩阵的稀疏矩阵。K = (K+K')/2 是为了确保总体刚度矩阵是完全对称阵,因为这会影响到MATLAB求解有限元方程时使用的算法,当K是实对称正定矩阵时MATLAB采用“Cholesky平方根分解法”求解,如果K不是对称正定则采用速度更慢的“LU三角分解法”。
下面这段测试程序很好地展示了LU分解和对称正定矩阵的Cholesky分解在MATLAB中运行效率的差距。 不难发现,88行程序始终围绕着“高效”,作者也为此下了很多功夫。
?
88行程序提供了两种滤波方法,指定ft=1时使用敏度滤波,指定ft=2时使用密度滤波。
注意这里其实分了两段,这是因为密度滤波并不是一次性完成的,在循环体外先根据链式法则对目标函数和体积约束的灵敏度信息进行修正,然后循环体内对设计变量进行密度滤波得到单元伪密度。
而敏度滤波就要简单的多,设计变量就代表单元伪密度,直接对目标函数的灵敏度信息进行滤波就可以。
在密度滤波中,引入了“设计变量(Design Variables)”和“物理密度(Physical Density)”两个场,在程序中的符号分别是x和xphys。这种情况下,设计变量并不代表真实的单元伪密度场,经过滤波的物理密度才是真实的单元伪密度场。包括之后的OC优化准则法迭代过程中,拉格朗日算子lmid也是由真实物理密度xphys决定的。在推导目标函数/约束条件关于设计变量的灵敏度信息时,必须使用链式法则来确定,参见论文公式(10)。
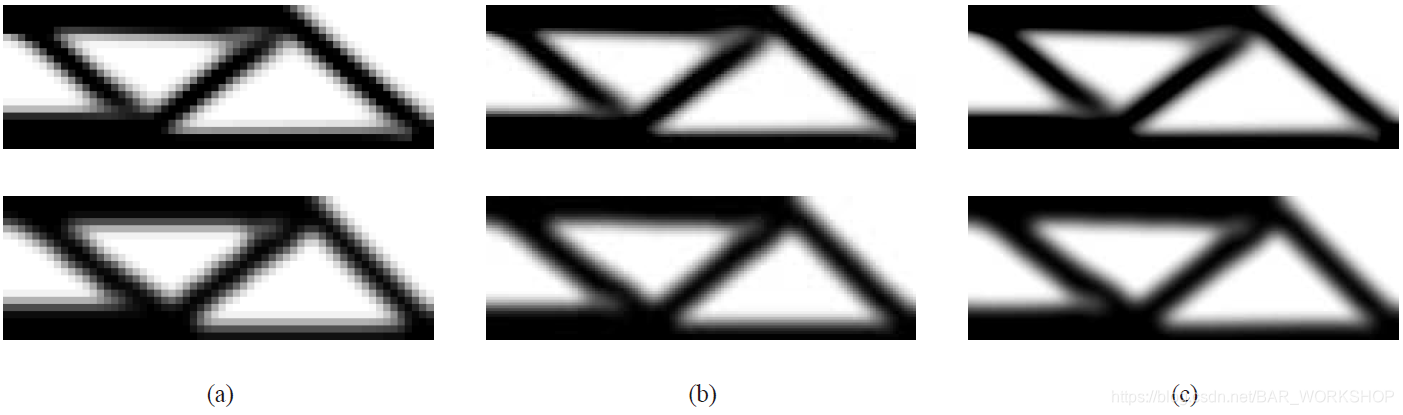
(a)60 X 20;(b)150 X 50;(c)300 X 100
上面三幅图像是使用敏度滤波得到的结果,下面三幅图像是使用密度滤波得到的结果
?
读完了99行程序和针对99行改进的88行程序,就让我们一起来对比测试一下吧。把下面这段程序加进主程序前后,正常运行一下就得到结果啦。我用一个90*30的网格就在笔记本上简单跑了一遍,结果来看88行程序在效率上的提升还是很显著的,几乎只用了99行六分之一的时间。
虽然在前面我们已经提到过好几次这段程序提高MATLAB运行效率的方法,这里我们再总结一下吧:
- 尽量减少for循环,培养矢量化思路;
- 为数组预分配内存空间;
- 尽量选用合适的MATLAB函数,这一点很宽泛,需要很多积累才行,这里我们至少知道了一条,Cholesky比LU快;
- 尽量避免频繁调用子程序;
- 精简循环体,能放在外面的代码就放到循环外面。
关于MATLAB的效率优化我一直想写一篇博客,可是我懒,涉及到太多方面一直不想动手写,hhh我尽快。
?
版权声明:本文为博主原创文章,转载请附上原文出处链接和本声明。
本文链接:http://blog.csdn.net/BAR_WORKSHOP/article/details/108287668



